赵育林教授团队荣获广东省科学技术奖自然科学 - 自然科学史研究杂志社投稿

一、来稿必须是作者独立取得的原创性学术研究成果，来稿的文字复制比（相似度或重复率）必须低于用稿标准，引用部分文字的要在参考文献中注明；署名和作者单位无误，未曾以任何形式用任何文种在国内外公开发表过；未一稿多投。二、来稿除文中特别加以标注和致谢之外，不侵犯任何版权或损害第三方的任何其他权利。如果20天后未收到本刊的录用通知，可自行处理(双方另有约定的除外)。三、来稿经审阅通过，编辑部会将修改意见反馈给您，您应在收到通知7天内提交修改稿。作者享有引用和复制该文的权利及著作权法的其它权利。四、一般来说，4500字（电脑WORD统计，图表另计）以下的文章，不能说清问题，很难保证学术质量，本刊恕不受理。五、论文格式及要素：标题、作者、工作单位全称(院系处室)、摘要、关键词、正文、注释、参考文献(遵从国家标准：GB\T7714-2005，点击查看参考文献格式示例)、作者简介(100字内)、联系方式(通信地址、邮编、电话、电子信箱)。六、处理流程：（1）通过电子邮件将稿件发到我刊唯一投稿信箱（2）我刊初审周期为2－3个工作日，请在投稿3天后查看您的邮箱，收阅我们的审稿回复或用稿通知；若30天内没有收到我们的回复，稿件可自行处理。（3）按用稿通知上的要求办理相关手续后，稿件将进入出版程序。（4）杂志出刊后，我们会按照您提供的地址免费奉寄样刊。七、凡向文教资料杂志社投稿者均被视为接受如下声明：（1）稿件必须是作者本人独立完成的，属原创作品（包括翻译），杜绝抄袭行为，严禁学术腐败现象，严格学术不端检测，如发现系抄袭作品并由此引起的一切责任均由作者本人承担，本刊不承担任何民事连带责任。（2）本刊发表的所有文章，除另有说明外，只代表作者本人的观点，不代表本刊观点。由此引发的任何纠纷和争议本刊不受任何牵连。（3）本刊拥有自主编辑权，但仅限于不违背作者原意的技术性调整。如必须进行重大改动的，编辑部有义务告知作者，或由作者授权编辑修改，或提出意见由作者自己修改。（4）作品在《文教资料》发表后，作者同意其电子版同时发布在文教资料杂志社官方网上。（5）作者同意将其拥有的对其论文的汇编权、翻译权、印刷版和电子版的复制权、网络传播权、发行权等权利在世界范围内无限期转让给《文教资料》杂志社。本刊在与国内外文献数据库或检索系统进行交流合作时，不再征询作者意见，并且不再支付稿酬。九、特别欢迎用电子文档投稿，或邮寄编辑部,勿邮寄私人，以免延误稿件处理时间。

赵育林教授团队荣获广东省科学技术奖自然科学

作者:

关键词:

摘要：

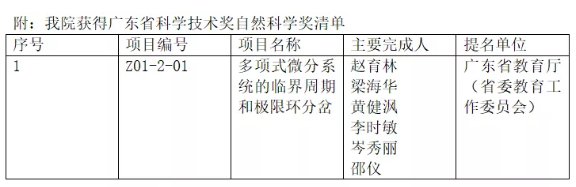
3月25日，广东省科技创新大会颁布了2019年度广东省科学技术奖。中山大学数学学院(珠海)赵育林教授牵头完成的科研项目“多项式微分系统的临界周期和极限环分岔”荣获广东省科学技术奖自然科学奖二等奖。

该项目属于常微分方程定性理论领域，主要研究平面微分系统的临界周期和极限环分岔，这是人们在研究希尔伯特第16问题过程中提出的两个核心课题。项目组以阿贝尔积分、复方程解析理论和微分几何为主要工具，探索了近年来广受关注的多类微分系统的闭轨族的周期变化规律和极限环分岔现象，并研究了某些高次微分系统的全局拓扑结构。为了便于数值计算和仿真，还探讨了离散系统存在周期解的条件。所取得的主要成果包括:证明了二次微分系统的余维4中心的周期是严格单调变化的;给出了若干二次微分系统临界周期的单调变化规律;证明了二次余维4系统受到摄动后产生的极限环个数不超过5，改善了“上界不超过8”的结论;推导出三类具有亏格1中心的平面系统的极限环个数的上界、给出一类分段光滑微分系统的分支函数，为解决其极限环问题提供了新的工具;给出了四次拟齐次多项式系统的所有全局相图，揭示其蕴含的所有动力学现象。作为应用，项目还探讨了平面食草动物与有毒植物共存的生态模型的极限环分岔现象。项目的开展丰富了微分动力系统的定性理论，发展了多个新方法。

广东省科学技术奖旨在奖励在推动科学技术进步活动中作出突出贡献的公民、组织，调动广大科技工作者的积极性和创造性，加速科学技术进步和促进经济建设与社会发展。每年评审一次。2019年度共颁发广东省科学技术奖自然科学奖一等奖12项，二等奖12项;技术发明奖一等奖9项，二等奖5项;科技进步奖特等奖1项，一等奖29项，二等奖105项;外加突出贡献奖2名，科技合作奖4名。

据悉，本次大会中山大学共获得24项科学技术奖，其中自然科学奖一等奖4项，二等奖3项;技术发明奖二等奖2项;科技进步奖一等奖2项，二等奖4项。